How much superposition is there?
Written as part of MATS 7.1. Math by Claude Opus 4.6.
I know that models are able to represent exponentially more concepts than they have dimensions by engaging in superposition (representing each concept as a direction, and allowing those directions to overlap slightly), but what does this mean concretely? How many concepts can "fit" into a space of a given size? And how much would those concepts need to overlap?
This felt especially relevant working on SynthSAEBench, where we needed to explicitly decide how many features to cram into a 768-dim space. We settled on 16k features to keep the model fast - but does this lead to enough superposition to be realistic? Surely real LLMs have dramatically more features and thus far more superposition?
As it turns out: yes, 16k features is plenty! In fact, as we'll see in the rest of this post, 16k features in a 768-dim space actually leads to more superposition than trillions of features in a 4k+ dim space, as is commonly used for modern LLMs.
Personally I found the answers to this fascinating - high dimensional spaces are extremely mind-bending. We'll take a geometric approach and try to answer this question. Nothing in this post is ground-breaking, but I found thinking about these questions enlightening. All code for this post can be found in on Github or Colab.
Quantifying superposition
First, let's define a measure of how much superposition there is in a model. We'll use the metric mean max absolute cosine similarity,
This metric represents a "worst-case" measure of superposition interference for each vector in our space. It's answer the question: on average, what's the most interference (highest absolute cosine similarity) each vector will have with another vector in the space?
Superposition of random vectors
Perfectly tiling the space with concept vectors is challenging, so let's just consider the superposition from random vectors (We'll see later that this is already very close to perfect tiling). If we have
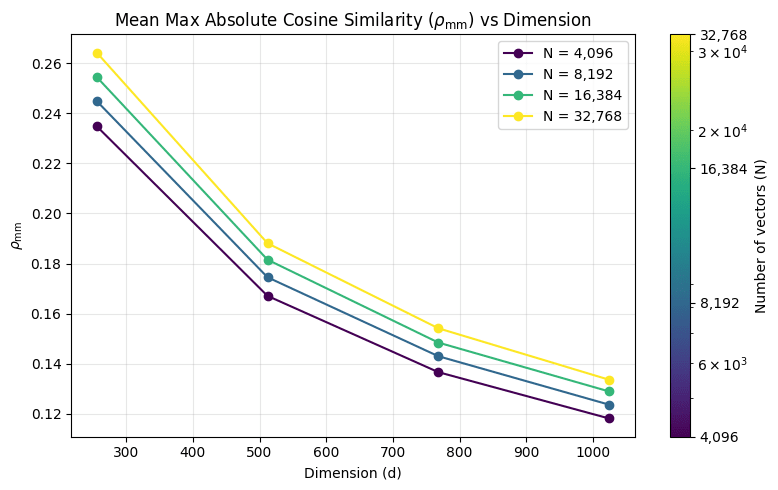
We vary
Calculating
We can compute the expected
For two random unit vectors in
For each vector, its max absolute cosine similarity with
We can calculate this integral using scipy.integrate. Let's see how well this matches our simulation:
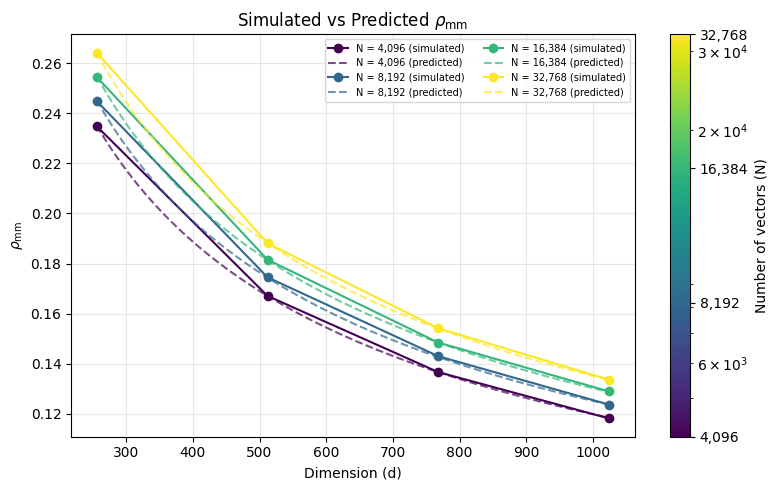
The predicted values exactly match what we simulated!
Scaling to trillions of concepts
Let's use this to see how much superposition interference we should expect for a some really massive numbers of concepts. We'll go up to 10 trillion concepts (10^13) and 8192 dimensions, which is the hidden size of the largest current open models. 10 trillion concepts seems like a reasonable upper bound for the max number of concepts that could conceivably be possible, since that would be roughly 1 concept per training token in a typical LLM pretraining run.
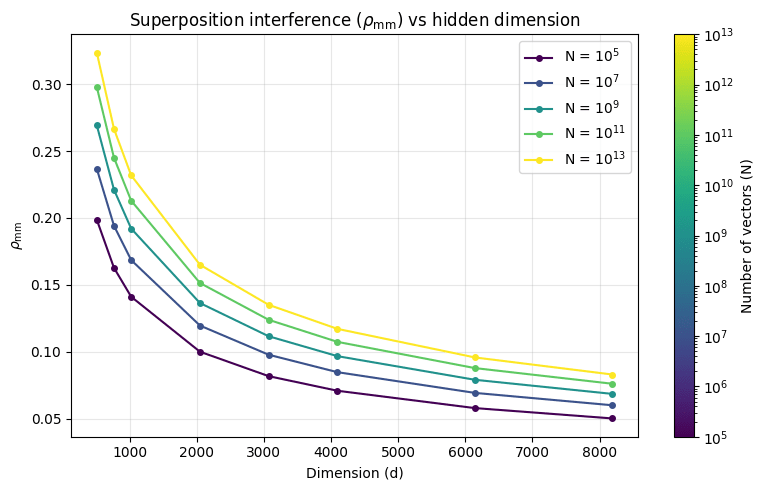
10 trillion concepts in 8192 dimensions has far less superposition interference than just 100K concepts in 768 dimensions (the hidden dimension of GPT-2)! That's a 100,000,000x increase in number of concept vectors! Even staying at a given dimension, increasing the number of concepts by 100x doesn't really increase superposition interference by all that much.

What if we optimally placed the vectors instead?
Everything above assumes random unit vectors. But what if we could arrange them optimally — placing each vector to minimize the worst-case interference? Would we do significantly better?
From spherical coding theory, the answer is: barely. The minimum achievable max pairwise correlation for
The intuition is that each vector "excludes" a spherical cap around itself, and we're counting how many non-overlapping caps fit on the unit sphere in
When
which gives:
This is exactly the leading-order term of the random vector formula! So random placement is already near-optimal — there's essentially nothing to gain from clever geometric arrangement of the vectors, at least for the
This is a remarkable consequence of high-dimensional geometry: in spaces with hundreds or thousands of dimensions, random directions are already so close to orthogonal that you can't do meaningfully better by optimizing.
What does this mean for SynthSAEBench-16k?
At the start, I mentioned that we used 16k concept directions in a 768-dim space for the SynthSAEBench-16k model. So is this enough superposition interference?
The answer is a resounding: yes. The SynthSAEBench-16k model has a
Discuss